Tempo de leitura: 6 minutos
Hoje, no mundo dos smartphones, serviços em nuvem e realidade aumentada, a Internet moderna com a qual contamos para dominar o mundo começa com algumas sequências simples de 1s e 0s, o que é realmente incrível.
Dessa forma, o binário, como é chamado de sistema simplificado e básico, é o predecessor que permitiu o desenvolvimento de todas as tecnologias modernas hoje.
Desde equipar máquinas decifradoras como o MK Ultra durante a Segunda Guerra Mundial, até permitir que o primeiro supercomputador do tamanho de uma sala execute e execute os cálculos necessários para enviar humanos à lua, até a realização de sistemas até mesmo simplificados como o binário. É realmente extraordinário.
Embora muitos cursos de codificação modernos sejam voltados especificamente para linguagens exigidas, como Python ou Golang.
Entender os fundamentos do binário e como ele funciona é quase como aprender suas letras e números antes de aprender a escrever artigos ou realizar cálculos matemáticos complexos.
Isso ocorre porque, sob o capô do complexo hardware moderno e das linguagens de programação usadas para construir softwares e aplicativos modernos, a função real de tirar uma foto com uma câmera digital ou recuperar informações de um banco de dados ainda aparecerá como um fluxo infinito de binários números (Bit) como:
01100100100010110101101010 (e assim por diante).
Portanto, antes de concluir seu curso de programação atual e começar a projetar o próximo grande aplicativo de mídia social do mundo ou uma nova inovação em aprendizado de máquina, vale a pena fazer uma pausa e se certificar de que entendeu o que é binário e como funciona.
Vamos dar uma olhada rápida nos fundamentos dos arquivos binários e como eles suportam as funções mais complexas que a maioria das pessoas pensa quando pensa na Internet e na tecnologia moderna.
A origem do código binário
Nas décadas de 1940 e 1950, em resposta aos desafios técnicos e intelectuais da Segunda Guerra Mundial e da corrida espacial, todos os primeiros técnicos de informática trabalharam no nível de cargos.
Se o computador cometer um erro e o técnico avaliar o sistema e determinar que não é o resultado de um tubo de vácuo queimado, ele pode simplesmente substituir 0 por 1 em algum lugar e tentar novamente.
Na vida diária, a maioria das pessoas usa o sistema decimal (também conhecido como base 10).
A razão para isso não é surpreendente – os humanos têm dez dedos das mãos e dez pés.
Naturalmente, este é o sistema mais simples para contar e realizar aritmética básica.
Se tivermos 16 dedos, podemos usar um sistema de base 16. Na verdade, a IBM criou este sistema no início dos anos 1960, usando “números” de 0 a 9 e de A a F.
Conhecido como “hexadecimal”, tornou-se a notação fundamental para os mainframes IBM System / 360.
A razão é que quando uma instrução de 16 bits é representada por quatro caracteres hexadecimais, como 58F0 (instrução “carregar”), em comparação com 0101 1000 1111 0000, o programador pode facilmente lembrar e usá-la. Seu nível mais baixo.
A utilidade do código binário
O conceito binário básico segue o princípio de que certas coisas estão ativadas ou desativadas, fornece algumas vantagens estruturais e torna a lógica (mesmo a lógica complexa) mais fácil de criar.
Ele se originou do trabalho de um matemático inglês chamado Charles Bull, que publicou um sistema lógico que foi o predecessor da lógica que alimenta todos os hardwares e softwares de computador.
O sistema de Boole inclui as operações básicas AND, OR e NOT, que podem formar sentenças simples com atributos binários (ou seja, se são verdadeiros ou falsos).
Além disso, esses elementos podem ser combinados e empilhados na estrutura lógica mais complexa.
As operações AND, OR e NOT podem ser facilmente integradas ao hardware na forma de “portas”.
Por exemplo, uma porta NOT (chamada de inversor) recebe a entrada 1 (ou 0) e então produz a saída oposta 0 (ou 1).
Da mesma forma, se uma ou duas entradas são 1, a porta OR gera 1, e se nenhuma das entradas é 1, ela gera 0.
Em seguida, essas portas podem ser combinadas de várias maneiras para fazer unidades aritméticas para adição, subtração, multiplicação e divisão.Depois de combinar portas suficientes, você tem a lógica básica por trás do computador.
Portas booleanas foram implementadas nos primeiros computadores com relés eletromecânicos (chaves físicas abertas ou fechadas), e posteriormente implementadas em máquinas modernas com transistores.
Micro chaves (pequenos interruptores) também seguem propriedades binárias liga / desliga.
Com base no trabalho de Boolean, Claude Shannon demonstrou em 1937 como a lógica booleana é realizada automaticamente por circuitos de comutação.
Lógica booleana pode resolver o problema simplesmente processando os dois símbolos 1 e 0.
Em 1948, Shannon, mais tarde conhecido como o pai da teoria da informação, provou que todas as informações podem ser representadas por zero e um, o que abriu um precedente na época e levou à rápida inovação e expansão do mundo da computação.
Os projetos Mercury, Gemini e Apollo eventualmente levaram ao mundo da computação doméstica desenvolvido por Bill Gates, Steve Jobs e outros.
Funções binárias
Comparado com o sistema decimal, o sistema decimal inclui 10 dígitos, e cada posição do dígito representa uma potência de 10 (por exemplo, 100 ou 1000, etc.).
No sistema binário, cada posição do dígito representa uma potência de 2 (4, 8, 16, etc.) Espere).
O sinal binário codificado é, na verdade, uma série de pulsos elétricos que representam os vários números, caracteres e operações a serem realizadas.
Dispositivos chamados relógios transmitem pulsos regulares, e então componentes chamados transistores (aqueles mencionados acima) são ligados (1) ou desligados (0) para realmente passar ou bloquear o pulso.
No caso do código binário, cada número decimal (0-9) é realmente representado por um conjunto de quatro dígitos binários, que são chamados de bits.
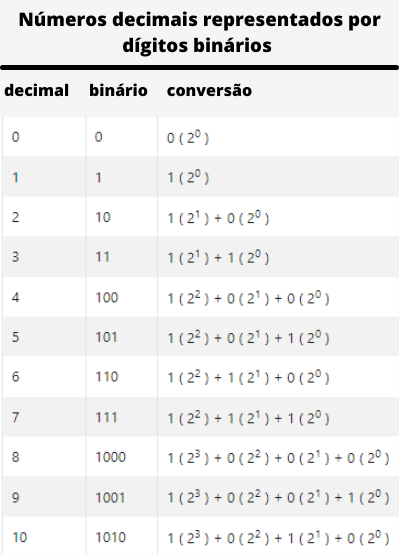
Portanto, as quatro operações aritméticas básicas (adição, subtração, multiplicação e divisão) podem ser simplificadas em uma combinação de operações básicas de álgebra booleana em números binários.
A tabela a seguir fornece uma representação de como será essa conversão.